|
John
Legon's Vanishing Point Update - September 2005
Giza Pyramid Vanishing Point Circle relationships
(This page is for archival purposes, please
access
the Mr. Legon's existing page here.)
Following a recent
discussion with Stephen Goodfellow, I've been taking another
look at the Giza Vanishing Point, and have been checking my
original calculations with the help of a CAD program. I have
also been looking again at the anomalous boundary wall to
the south of the Third Pyramid, and its connection with the
two encompassing circles of the three pyramids.
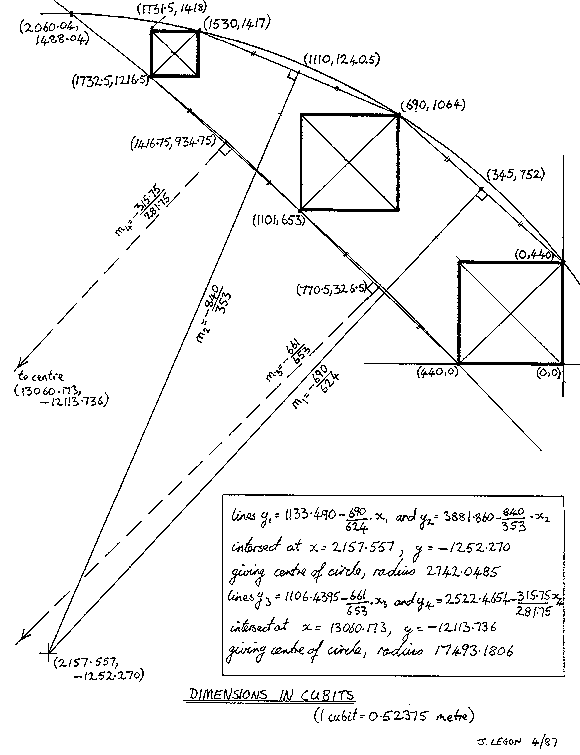
In my original computation of the Vanishing Point, I used
analytical geometry to determine the centres of the circles,
based upon the coordinates of the pyramid-corners through
which the circumferences of the two circles had to pass.
Those coordinates were expressed in terms of Egyptian royal
cubits, measured southwards and westwards from the
north-east corner of the Great Pyramid, as determined by my
analysis of the
Giza
Site Plan. Essentially, the coordinate points
represented a conversion into cubits of Petrie's survey data
in inches, although Petrie himself did not think that a
connection between the three pyramids had been planned. The
centres of the circles were obtained from the points of
intersection of the perpendicular bisectors of the notional
chords which can drawn between the respective corners of the
three pyramids, as detailed in my original diagram below:
|
 |
With the assistance of
CAD, it is a relatively simple matter to determine the
dimensions of circles passing through any three points, given
the coordinates, and hence to confirm that the results of the
calculations which I carried out back in April 1987 are correct.
Note that the above diagram was sent to Stephen for his own
information. If I had known that it would later appear on his
web site (and now on my own), I might have taken more care with
my handwriting....
The following diagram shows where the centres of the two circles
are located in relation to the three pyramids. Only a portion of
the larger circle has been drawn, since the dimensions are too
vast for the full circumference to be represented effectively on
the same scale as the pyramids themselves. |
 |
Now with regard to the
dimensions of these circles, I had always taken the view that
they were coincidental by-products of the Giza Site Plan,
without any real significance of their own. After all, it seemed
highly unlikely that the architect of the site plan could have
calculated the radii and the centres, let alone have configured
the layout to obtain specific results. In any case, I had
already ascribed the exact dimensions and relative positions of
the three pyramids to a highly logical and coherent design, in
which every measurement had been explained and often with
reference to more than one requirement. There was little reason
to think that any further factors had to be taken account -
least of all two circles of enormous size.
However, there was a nagging suspicion that my preconceptions
were not entirely justified. From the outset, one or two of the
dimensions were clearly significant, as I mentioned to Stephen
in a letter many years ago. It was exceedingly strange that the
centre of the large circle was just 11,000 cubits southwards
from the vanishing point itself, with a computed discrepancy of
only 0.13 cubit. Not only did the chances of randomly obtaining
such a round number with such accuracy seem rather slight, but
the number was significant in its own right. In the Giza plan,
as we have seen, the modular design placed the south side of the
Second Pyramid 1100 cubits southwards from the north side of the
Great Pyramid, so that the north-south dimension encompassing
these two pyramids was just 5/2 times the base of the Great
Pyramid of 440 cubits. In addition, the coordinates of the
vanishing point and the radius of the small circle corresponded
to whole numbers of cubits to within 0.05 cubit, and although
not particularly interesting, conformed to the cubit system.
It was only recently, however, that some
further relationships came to light, when Stephen pointed out
that the circumference of the large circle was just 20 times the
diameter of the small circle. The exact factor of 20.04 was
close enough to a round figure to suggest deliberate intent. Now
for the reasons outlined above, I hadn't paid much attention to
the dimensions of the circles, and cannot recall having
calculated the circumferences. I knew that the radius of the
large circle corresponded to a round 17,500 cubits, with a
discrepancy of only 0.04%, but had declined to draw any further
conclusions. The diameter of the large circle is, however,
practically just 35,000 cubits, so that given the approximation
to p of 22/7, the circumference will be 110,000 cubits.
Not only is it inherently quite surprising to obtain these
simple multiples of 10,000
cubits, but the circumference is also just
10 times the distance
northwards from the centre of the circle to the Vanishing Point
- through which, by definition, the circumference must pass.
Once again, therefore, it is not just the whole numbers of
thousands of cubits which are significant, but the fact that
these dimensions are mathematically meaningful. Being a multiple
of 7000 cubits, the diameter of 35,000 cubits would have been an
ideal choice - if indeed it was chosen - since the circumference
would also contain a round number of thousands of cubits,
according to the 'classic'
value for p of 22/7. The same reasoning applies also
to the Great Pyramid, which is thought to embody the p-proportion
through its height of 280 cubits and side-length of 440 cubits.
Furthermore, the circumference of the large circle is just 250
times the side-length of the Great Pyramid, and the dimensions
of 440 and 250 cubits are consecutive in the Giza plan.
It must be noted that the diameter of the large circle is highly
sensitive to the exact placing of the pyramid corners through
which the circumference passes, owing to the flatness of the
curve which connects them. Indeed, if the three corners had been
placed in a straight line, then that line would belong to the
circumference of a circle with infinite radius. Although the
slight bend in the line reduced the diameter to a 'sensible'
dimension, the dimension changes rapidly with slight adjustments
of the pyramid corner positions. It turns out - and I still find
this hard to believe - that the precise diameter of 35,000
cubits can be obtained for the large circle by shifting the
south-east corner of the Second Pyramid a mere 0.006 of a cubit
from the position as defined by the site-plan coordinates in
whole cubits!
If it had ever been intended to define a circle with a diameter
of 35,000 cubits by means of the three pyramid-corners,
therefore, then it would have been virtually impossible to
achieve a more accurate result than that actually obtained by
the site-plan dimensions. It is true that the circumference of
the circle will not be exactly 110,000 cubits if the exact value
of p is used instead of 22/7, yet the relationship with
the Great Pyramid still stands, since the dimensions of this
pyramid arguably reflect p with greater accuracy than
22/7.
Now turning to the small circle, my computations had shown that
the radius was 2742 cubits, while the centre was 2740 cubits
eastwards from the Vanishing Point. This number was significant
to me as being practically ten times the height of the Second
Pyramid, which the survey-data and theoretical factors had shown
to be 274 cubits. Whilst the dimensions of the large circle
seemed to refer to the Great Pyramid, therefore, a comparable
relationship existed between the small circle and the Second
Pyramid. At the same time, the diameter of the small circle is a
fair approximation to one-twentieth of the circumference of the
large circle, as Stephen suggested - this requiring a radius of
about 2748 cubits.
The Boundary Wall
We have already referred to the anomalous boundary wall to the
south of the Third Pyramid, which seems to run straight over the
Vanishing Point. Stephen wanted to know whether the wall
described a large circle, and whether it was possible - given
the fragment that exists - to accurately determine the size of
the circle. It might be interesting at this point to quote from
a letter I sent Stephen on 16th April 1987: |
| There are a few
strange things about this wall, the first being that while all
the other boundary walls at Giza are aligned north-south or
east-west, this wall diverges by about 7 degrees from an
east-west alignment - in such as way as to just encompass the
vanishing point within the boundary. Secondly, this wall was not
built in a straight line but in fact represents the arc of a
very large circle, the radius of curvature of which is in the
region of 11000 cubits - or comparable to the larger of your two
ground circles. A chord joining the ends of this curved section
of boundary wall actually falls precisely on the point of
intersection of the two ground circles, which point would
therefore have been covered over if the wall had been built in a
straight line! |
| Although at that time I had
answered Stephen's question, I now find that the details are not
quite correct. The rough figure of 11,000 cubits which I gave
for the radius of curvature of the wall, actually referred to
the diameter! Apart from this simple mistake, much depends on
the accuracy of Petrie's plan of the boundary wall, upon which I
had based my calculations. In a letter dated 27th May 1987, I
wrote: |
| These walls were all
surveyed more than a hundred years ago by Flinders Petrie, who
was also puzzled by the line of the southern wall and wrote: "it
is impossible to suppose its skew and bowing line to have been
laid out along with the very regular lines of the other parts."
Yet this wall is of the same construction, and its curvature
must have been produced by a deliberate effort of the builders -
so I think it must definitely have had a special significance.
|
Looking again at Petrie's work,
it is clear that he took great trouble to determine the exact
lines of the walls around the Third Pyramid, as he says: "They
were all fixed in the survey by triangulation, with more
accuracy than the wall-surface can be defined." In my
reassessment of the curvature of the south boundary wall, I took
a scan of Petrie's plan, and determined the coordinates in
pixels of three points along the wall - at either end and at the
approximate mid-point. These coordinates were then related to
the size and position of the Third Pyramid, scaled to the
dimensions of the Giza plan in cubits, and entered into the CAD
program. This gave a radius of curvature of around 4800 cubits.
As a check on this estimation, I imported the scan into the CAD
program, and scaled and positioned it so that the base of the
Third Pyramid matched the site-plan location. By this means, I
could not only determine the centre and radius of the circle,
but also superimpose the accurately-plotted circumference on
Petrie's plan, in order to make a comparison with the curvature
of the wall as it was actually built. As can be seen in the
diagram below, in which the arc of the circle is shown in
magenta, the agreement with the line of the wall is rather
close, being in fact practically pixel-perfect:
|
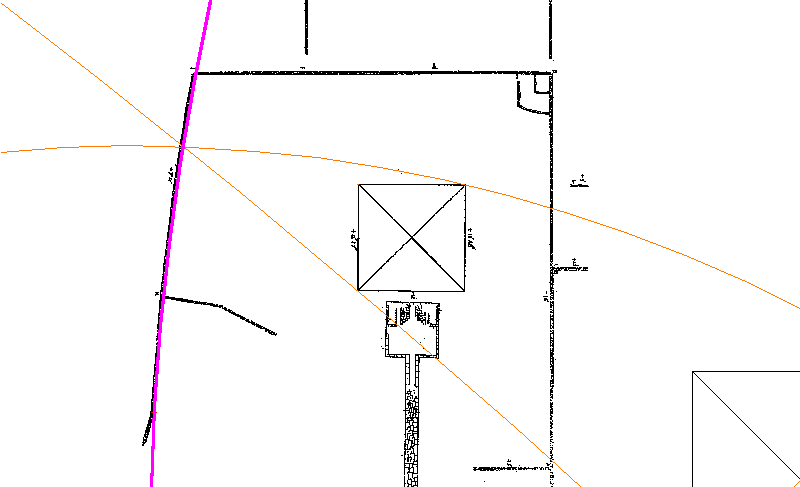
This new evaluation also
confirmed that the Vanishing Point is extremely close to the
inner (north) side of the wall. It now appears that if the wall
had been built in an exact straight line between the ends of its
curvature, then the vanishing point would have been just outside
the enclosure. Not only was the anomalous curve similar to that
of the pyramid ground circles, therefore, but the position of
the wall and the effect of the curve were significant in
relation to the vanishing point. At this stage, however, the
radius of curvature and the centre-point of the circle appeared
to be arbitrary. Clearly, the circle of the wall did not make
contact with the pyramids, or with any other structures as far
as I could see, so the question arose as to whether the size and
position had any significance of their own.
Again with the assistance of CAD, it was easy to plot the entire
circle and relate the dimensions to the vanishing point circles.
The result of this exercise is shown in the diagram below. Much
to my surprise, the circle of the wall was bounded to the east
and west by tangents to the small and large circles drawn
parallel to the north-south axis of the plan. Consequently, the
size and position of the wall circle were entirely a function of
the pyramid ground circles. First, the diameter and east-west
position of the wall circle are defined by the eastward extent
of the small circle, and by the westward extent of the large
circle, thus being equally dependent upon both circles. Second,
the north-south position of the wall circle is such that the
circumference intersects the vanishing point, which is itself
defined by the intersection of the pyramid ground circles: |
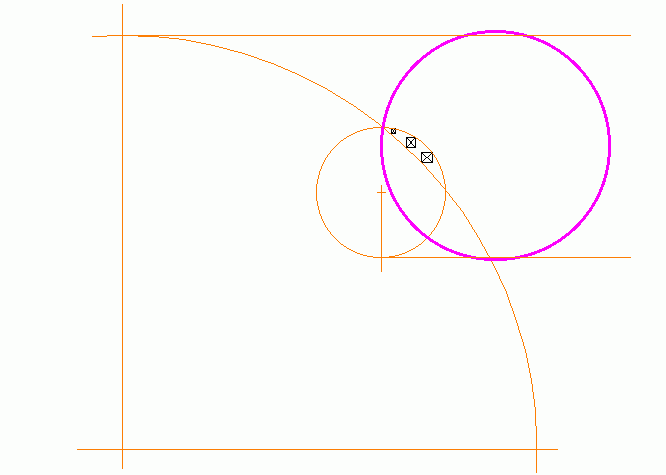
It will noted that there is a
slight discrepancy between the circumference of the wall circle
and the tangents as drawn to the small and large circles. Given,
however, that the wall circle had to be extrapolated from a
fairly short segment, the agreement seems remarkably good. It
is, of course, possible to construct a theoretical circle which
is defined exactly by the tangents to the pyramid circles; and
when overlaid on the wall as built, the departure is no greater
than the thickness of the wall itself.
Now as Stephen will confirm, I have always been extremely
skeptical about the idea that the pyramid-builders had intended
to lay out the Giza pyramids in such a way as to define anything
resembling a vanishing point. However, when all the evidence is
considered, it does seem to me that there is quite a strong
argument to support the idea that the builders were aware of the
fact that the three pyramids were bounded by circles which
defined two points by their intersection - one being comparable
to the artist's conception of a vanishing point. Perhaps after
the three pyramids had been built, the architects turned their
attention to the location of the boundary walls, which can be
shown to have been laid out on a definite plan. It was then,
perhaps, that the dimensions of the enclosing circles were
considered, and found to be of sufficient interest to justify
the enhancement of the unified plan by setting out the southern
enclosure wall in a manner which was entirely contrary to their
usual practice. For to construct a wall with such a continuous
but slight curve can only have been the result of conscious
effort...
John Legon, 17/09/05
( This page is for archival purposes - please
access the
existing page here.)
John Legon's
Home Page |
|

