>From pegasus.cau.edu!fsmith Fri May 10 01:39:28 1996
Date: Fri, 10 May 1996 01:43:06 -0400
From: Tony Smith <fsmith@pegasus.cau.edu>
Reply-To: fsmith@pegasus.cau.edu
MIME-Version: 1.0
To: esteban@goodfelloweb.com
Subject: apex
Status: R
Your apex vanishing point idea is very interesting.
Here are some very rough thoughts. I apologize for the
length of this message and the roughness of these
calculations, but they are 1-day back-of-the-envelope
calculations designed, not to prove a point conclusively,
but to explore whether more detailed calculations might
be worthwhile.
If you get a chance, let me know what you think.
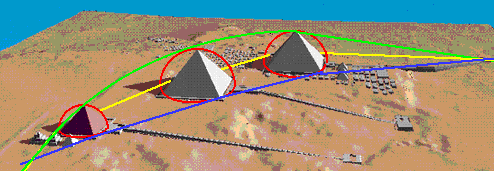
First, I put the ground-level vanishing point formed
by the intersection of the southeast base corner circle
and the northwest base corner circle at (or very near)
the southern boundary wall of the third pyramid.
As John Legon noted, that wall is not straight,
but curves in the arc of a circle of radius 11,000 cubits,
which is the radius of the southeastern corner circle.
Then, I set up a 3-dim coordinate system (x,y,z)
with origin (0,0,0) at the ground vanishing point.
Then, I very roughly estimated the 3-vectors (in cubits)
from the origin to the apex of each of the 3 pyramids:
Great Pyramid - (1840, 1268, 280)
Second Pyramid - (1164, 730, 272)
Third Pyramid - ( 430, 172, 125)
Now, if a circle through the 3 apex points goes through
the ground vanishing point, those 3 vectors should all
lie in the same plane.
To see if it does, take the determinant of the
3x3 matrix formed by the 3 vectors.
If the 3 vectors are in the same plane,
the determinant should be zero:
(1840, 1268, 280)
(1164, 730, 272)
( 430, 172, 125)
I got roughly 357 - 371 = - 14,
which is close enough to zero for these very rough calculations.
Now, consider the apex plane containing those 3 vectors.
It contains the ground vanishing point and the 3 apex points.
It also intersects the ground (horizontal) plane.
The apex plane and the ground plane intersect in a line.
To find the line, note that any vector in the ground plane
is of the form (x, y, 0) because it can be anywhere
on the ground (x and y) but is at ground level (z = 0).
You can find the equation for the intersection line by
making a determinant of a ground vector (x, y, 0)
with two of the apex vectors and setting
that determinant equal to zero.
In effect, that requires the unknown ground vector (x, y, 0) to
lie in the apex plane, and therefore to be in the
intersection of the apex plane and the ground plane.
You get, for example, if you use the Third Pyramid,
the Great Pyramid, and the ground vector,
the determinant of the matrix:
( 430, 172, 125)
(1840, 1268, 280)
( x, y, 0)
which is roughly
48,000 x + 220,000 y - 158,000 x - 120,000 y = 0
or
100,000 y - 110,000 x = 0
or
a line leading from the origin (vanishing point)
of slope roughly
y = 1.1 x
Now look at the southeast corner of the base of the Great Pyramid.
Its coordinates (from the vanishing point origin)
are (1620, 1488, 0)
which gives a slope of roughly y = 0.9 x
that is close enough to be interesting.
If the intersection line does go through the southeast corner
of the base of the Great Pyramid, then
the intersection line is a chord of your southeastern corner circle,
which has a radius of 11,000 cubits,
which is the radius of the curved southern boundary wall of the
Third Pyramid, where the vanishing point is located.
Also, the angle between the apex plane and the ground plane
would be the roughly about the angle of an edge of the Great Pyramid
with the ground (arris slope-angle), or about 42 degrees.
(How close it is to the 42 degrees is related to how close
the Great Pyramid southeast-northwest axis is to being
perpendicular to your southeastern corner circle.)
More detailed and accurate calculations may refute these ideas,
but they are interesting to me and I thought you might like to
see them.
Tony 10 May 96
>From pegasus.cau.edu!fsmith Fri May 10 22:13:45 1996
Date: Fri, 10 May 1996 22:17:17 -0400
From: Tony Smith <fsmith@pegasus.cau.edu>
Reply-To: fsmith@pegasus.cau.edu
MIME-Version: 1.0
To: sgoodf@oeonline.com
Subject: more careful calculation
Status: R
More careful calculation seems so far to show that the
Apex circle interesects the ground level at a point
about 200 cubits away
from the ground level vanishing point of the base corners.
That is trying to take into account the base elevations of the 3
pyramids,
and using the middle pyramid base level as ground level.
I am going to work some more and check these results,
but for now it looks like my preliminary guesses did not
work out, and that John Legon was right.
I hope he gets internet access and e-mail soon.
Communication by snail-mail is very slow.
Thanks for the ideas, which are fun and interesting
even though my initial guesses seem to be wrong.
Tony 10 May 96
>From pegasus.cau.edu!fsmith Sat May 11 11:58:12 1996
Date: Sat, 11 May 1996 12:01:50 -0400
From: Tony Smith <fsmith@pegasus.cau.edu>
Reply-To: fsmith@pegasus.cau.edu
MIME-Version: 1.0
To: sgoodf@oeonline.com
Subject: apex again
Status: R
There is a way to make the apex vanishing point work,
using a slightly different point of view.
Why were the pyramids built with a Golden proportion?
So that they each "squared the circle",
that is,
the total circumference of the base is
the circumference of a circle whose radius is
the height of the pyramid.
So, what you should do is to take a sphere whose
center is the center of the base of the pyramid
and whose radius is the height of the pyramid.
The top of the sphere is then the apex of the pyramid.
Then, instead of running your perspective circle curves
through the corners of the square base,
(which John Legon shows is inconsistent with a
perspective circle through the center, or apex projected to the
ground)
you should run your perspective circle curves through:
1. the center of the sphere, which is also the center of the
equatorial circle at ground level, which is also
the apex projected to the ground;
2. the outer perspective circle should be tangent to the
outside of the equatorial circle of the sphere of each pyramid;
3. the inner perspective circle should be tangent to the
inside of the equatorial circle of the sphere of each pyramid.
I think that this guarantees that all three perspective circles will
meet at the same vanishing point, at least if you project
everything to one ground level and ignore elevation.
I will think about whether elevation should be considered.
Maybe so, because it is there.
Maybe not, because the distance to the stars is not usually
considered in a star map. The patterns are just projected flat.
Same with most earth geographic maps.
What this point of view does,
is take the square base, ignore its corners,
and round it to a circle, and use the circle,
which is what the builders seemed to want you to do
by using the Golden ratio design.
The problem with the original way of doing the vanishing point
was not the apex (it is correct) but was the use of corners
of the square instead of tangents to the circle that
was squared by the square.
This vanishing point will be a little different from the
corner one calculated by John Legon. Maybe he could do
some accurate calculations from this point of view,
if he finds it interesting.
I like the vanishing point idea.
One interesting speculative thing:
if you use it with my star pattern (Vela X, Sirius, Betelgeuse)
for the pyramids, you would get another point (not seen when
the pyramids were built, because no monument is there).
That point is roughly in the Milky Way to the north of
Betelgeuse, which is roughly where the Crab Nebula pulsar
is located. It was a supernova that exploded about 7,500 years ago,
but is about 6,500 light years away, and was not seen on
Earth until about 1,000 years ago, on 4 July 1054 AD,
and therefore it also not seen when the pyramids were built.
(I will again check my rough estimates, which
as you know can be wrong.)
Tony 11 May 96
|
